Nachdem ich im ersten Beitrag die Grundlagen der Quantenphysik erläutert habe, werde ich in diesem Beitrag versuchen, die grundlegende Mathematik möglichst einfach zu erklären. Spätestens wenn wir uns manche Eigenschaften wie die Verschränkung oder Quantenteleportation anschauen, dann wird die Thematik mit etwas Mathematik erheblich leichter verständlich. Vorab der übliche Disclaimer: Ich bin weder Mathematiker, noch Physiker. Aus diesem Grund werde ich sicherlich nicht alle Punkte mit mathematisch/ physischer Präzision korrekt formuliert darlegen können. Insofern du Verbesserungsvorschläge für die Beiträge hast, so freue ich mich selbstverständlich über einen Kommentar oder Feedback.
| Dieser Artikel ist Teil einer Serie:
- Teil 1: Was ist Spin? |
Kapitel 1: Zahlenmengen
Beginnen wir mit dem ersten Thema: Zahlenmengen. Zahlenmengen werden die meisten von uns sicherlich schon einmal im Laufe der Schulzeit gehört haben. So gibt beispielsweise die natürlichen Zahlen, ganze Zahlen oder auch die rationalen Zahlen. Da es ein Großteil der Literatur zu Quantentheorien primär auf englisch gibt, werde ich die wichtigsten englischen Übersetzungen im Folgenden ergänzen, um eine Recherche zu Details zu erleichtern.
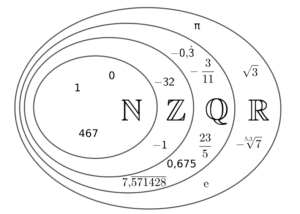
Eine kurze Wiederholung der bekanntesten Zahlenmengen:
Natürliche Zahlen, mathematisch mit 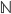 zusammengefasst, sind alle positiven ganzen Zahlen, je nach Definition mit oder oder Null:
zusammengefasst, sind alle positiven ganzen Zahlen, je nach Definition mit oder oder Null:
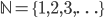
Ganze Zahlen, mathematisch 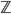 , sind eine Erweiterung der natürlichen Zahlen und umfassen sämtliche ganze Zahlen:
, sind eine Erweiterung der natürlichen Zahlen und umfassen sämtliche ganze Zahlen:
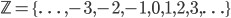
Rationalen Zahlen, mathematisch 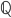 , sind Zahlen, die als Verhältnis zweier ganzer Zahlen, d.h. als Bruch, dargestellt werden können:
, sind Zahlen, die als Verhältnis zweier ganzer Zahlen, d.h. als Bruch, dargestellt werden können:
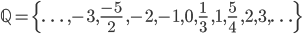
Reelle Zahlen, mathematisch 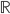 , erweitern die rationalen Zahlen um irrationale Zahlen. Irrationale Zahlen sind z.B. Zahlen, welche nicht ganzzahlige Wurzeln aus ganzen Zahlen wie
, erweitern die rationalen Zahlen um irrationale Zahlen. Irrationale Zahlen sind z.B. Zahlen, welche nicht ganzzahlige Wurzeln aus ganzen Zahlen wie 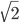 sind oder auch die Kreiszahl
sind oder auch die Kreiszahl 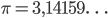 :
:
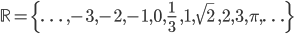
Komplexe Zahlen, mathematisch 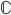 , erweitern den Zahlenbereich der reellen Zahlen so, dass die Gleichung
, erweitern den Zahlenbereich der reellen Zahlen so, dass die Gleichung 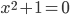 lösbar wird. Dies gelingt durch Einführung der imaginären Zahl
lösbar wird. Dies gelingt durch Einführung der imaginären Zahl 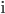 mit der Eigenschaft
mit der Eigenschaft 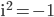 .
.
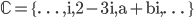
Komplexe Zahlen sind für das Verständnis der Quantenphysik äußerst relevant. Eine komplexe Zahl 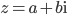 besteht stets aus einem Realteil (
besteht stets aus einem Realteil (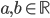 ) und einem Imaginärteil (
) und einem Imaginärteil ( ). Das Zeichen
). Das Zeichen  bedeutet "ist ein Element von".
bedeutet "ist ein Element von".
Wichtig ist hierbei die Kenntnis der komplexen Konjugation (complex conjugate) von 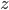 , also der Abbildung
, also der Abbildung
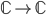
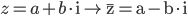
Für den Moment ist es ausreichend die gezeigte Formel mit der komplexen Konjugation zu verbinden, d.h. der imaginäre Teil wird negiert. Konjugierte Zahlen werden mit einem Oberstrich markiert, im Beispiel wurde aus 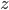 ein
ein 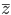 .
.
Im nächsten Kapitel werde ich über Vektoren sprechen, also Elemente eines Vektorraums. In der Schulzeit wurde dieses Thema bei vielen wahrscheinlich anhand von Pfeilen ("Vektoren") in einem zwei-oder dreidimensionalen Raum erläutert.
Kapitel 2: Vektoren
Ein Vektor in einem dreidimensionalen Raum kann beispielsweise wie folgt beschrieben werden:
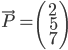
Vektoren werden in der Mathematik gerne mit einem Pfeil über den Vektor-Zeichen dargestellt: 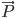 . In einem "klassischen" kartesisches Koordinatensystem würde der Vektor wie folgt visualisiert werden:
. In einem "klassischen" kartesisches Koordinatensystem würde der Vektor wie folgt visualisiert werden:
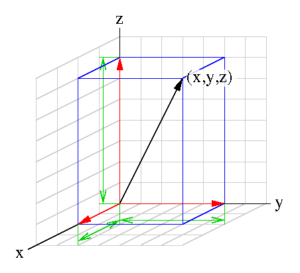
Der Vektor 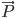 besteht in unserem Fall aus drei Komponenten - der x, y und z Komponente. Vom Ursprung aus könnten wir den Vektor nun zeichnen, indem wir 2 Einheiten entlang x-Achse, 5 Einheit entlang y-Achse und 7 Einheiten entlang der z-Achse gehen würden. Die Schreibweise selbst könnten wir verallgemeinern indem wir schreiben:
besteht in unserem Fall aus drei Komponenten - der x, y und z Komponente. Vom Ursprung aus könnten wir den Vektor nun zeichnen, indem wir 2 Einheiten entlang x-Achse, 5 Einheit entlang y-Achse und 7 Einheiten entlang der z-Achse gehen würden. Die Schreibweise selbst könnten wir verallgemeinern indem wir schreiben:
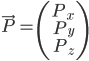
Hierbei gilt:  , d.h. der Vektor
, d.h. der Vektor 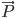 ist ein Element einer dreidimensionalen, reellen Zahlenmenge.
ist ein Element einer dreidimensionalen, reellen Zahlenmenge.
Eine etwas andere Schreibweise des Vektors, bei gleicher Bedeutung, ist die Folgende:
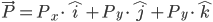
Der "Hut" auf einem Symbol bedeutet, dass es sich bei dem Wert um einen Einheitsvektor handelt. Ein Einheitsvektor ist ein Vektor der Länge 1. Die Berechnung der Länge eines Vektors wird mit dem Satz des Pythagoras vorgenommen - später mehr dazu. Die Symbole 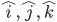 stehen stellvertretend für die folgenden Vektoren:
stehen stellvertretend für die folgenden Vektoren:
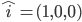
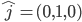
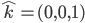
In den Klammern befinden sich auch diesem Fall die x, y und z Komponenten. Die genannten drei Vektoren werden in der Mathematik auch Basis-Vektoren genannt. Das initiale Beispiel wäre in diesem Fall wie folgt:
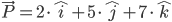
Anhand dieser Formel würde sich der Vektor ebenfalls sehr einfach zeichnen lassen:

Ja - es ist genau derselbe Vektor! Die Formel bedeutet: Gehe 2 Einheiten nach 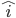 (= x), 5 Einheiten nach
(= x), 5 Einheiten nach 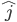 (= y) und 5 Einheiten nach
(= y) und 5 Einheiten nach 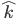 (= z). Die Bedeutung ist gleich - wichtig ist jedoch die Erkenntnis, dass sich ein Vektor auch in der letzteren Schreibweise beschreiben lässt.
(= z). Die Bedeutung ist gleich - wichtig ist jedoch die Erkenntnis, dass sich ein Vektor auch in der letzteren Schreibweise beschreiben lässt.
Kapitel 3: Berechnungen mit Vektoren
Mit dem nun gesammelten Wissen können wir jetzt bereits erste Berechnung vornehmen. Als erster Ausgangspunkt bietet sich die Berechnung der Länge eines Vektors an. Die Länge des Vektors 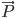 entspricht der Länge der schwarzen Linie
entspricht der Länge der schwarzen Linie 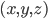 in der vorhergehenden Darstellung.
in der vorhergehenden Darstellung.
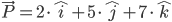
Die Länge dieses Vektors wird wie folgt berechnet:
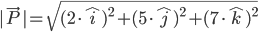
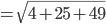
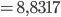
Zur Anwendung kommt in diesem Fall der Satz des Pythagoras. In einem zweidimensionalen Raum wurde dies in der Schule gerne mit der einprägsamen Formel 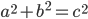 erläutert. Zur Darstellung der Länge eines Vektors
erläutert. Zur Darstellung der Länge eines Vektors 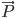 wird vor und nach dem Vektor ein |-Symbol eingefügt (
wird vor und nach dem Vektor ein |-Symbol eingefügt (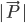 ).
).
Eine weitere spannende Berechnung ist das so genannte Skalarprodukt. Das Skalarprodukt gibt, vereinfacht ausgedrückt, die Lage zweier Vektoren zueinander an. Umgangssprachlich formuliert: "Inwiefern zeigen 2 Vektoren in dieselbe Richtung?"
Ein Beispiel:
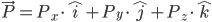
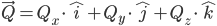
Durch eine simple Multiplikation miteinander kann das Skalarprodukt errechnet werden:
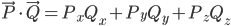
Verwenden wir beispielsweise in einem zweidimensionalen Raum zwei rechtwinklig zueinander stehende Vektoren
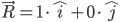
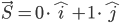
so wäre das Skalarprodukt
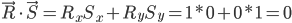 .
.
Je weiter 2 Vektoren in die gleiche Richtung zeigen, desto größer das Skalarprodukt.
Kapitel 4: Paul Dirac: Die Braket Notation
Im zweiten Kapitel haben wir über Vektoren gesprochen:
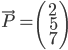
Das Konzept eines Vektors können wir weiter vereinfachen - ein Vektor selbst ist erst mal nichts weiter als eine Liste von Elementen. In der Quantenmechanik werden Vektoren mathematisch etwas anders als bekannt dargestellt - mit Hilfe der Braket-Notation:
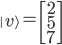
Insofern die Liste vertikal ausgerichtet ist, also als 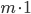 Matrix, so wird diese auch als ket bezeichnet. Kets werden in der Quantenphysik grundsätzlich mit dem Symbol
Matrix, so wird diese auch als ket bezeichnet. Kets werden in der Quantenphysik grundsätzlich mit dem Symbol 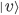 deklariert. Etwas generischer ausgedrückt wird ein ket wie folgt deklariert:
deklariert. Etwas generischer ausgedrückt wird ein ket wie folgt deklariert:
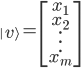
In der horizontalen Schreibweise, also als 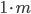 Matrix, wird die Matrix als bra bezeichnet. Bras werden grundsätzlich mit dem Symbol
Matrix, wird die Matrix als bra bezeichnet. Bras werden grundsätzlich mit dem Symbol 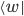 deklariert.
deklariert.
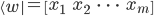
Die Braket-Notation geht auf Nobelpreisträger Paul Dirac zurück.

Die Braket-Notation wird zur Darstellung quantenmechanischer Zustände genutzt. Wichtig für den Moment: Die horizontale Schreibweise wird als bra, die vertikale Schreibweise als ket bezeichnet. Inhaltlich bleibt sie für den Moment eine mathematische Schreibweise eines Vektors in einem Raum. Ganz naiv könnten wir uns für den Moment einmal vorstellen, dass der Spin eines Elektrons wie ein Pfeil zu verstehen ist, der in einem dreidimensionalen Raum in eine beliebige Richtung zeigt.
Kapitel 5: Vektoren in der Welt der Quanten
Die Nutzung von Vektoren in der Quantenmechanik unterscheidet sich insbesondere an zwei Stellen von Vektoren, wie wir sie gerade beschrieben haben:
- Es wird mit komplexen Zahlen gerechnet (
 )
) - Es wird mit einem zweidimensionalen Raum gearbeitet (
 )
)
Ab diesem Moment ist es wichtig, gedanklich den Absprung weg von "klassischen" Vektoren zu schaffen. Es wird nicht funktionieren, die folgenden Rechnung der Quantenmechanik mit Hilfe eines "klassisch-dreidimensionalen" Raumes zu visualisieren. Letztendlich sprechen wir im Folgenden zwar weiterhin von einer x, y und z-Achse, die dritte Achse wird jedoch in der Quantenmechanik mit Hilfe der komplexen Zahlen ermöglicht.
Im vorherigen Kapitel haben wir von 3 Basisvektoren gehört: 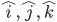 . Der Vektor
. Der Vektor 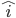 beschreibt die x-Achse, der Vektor
beschreibt die x-Achse, der Vektor 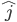 die y-Achse und der Vektor
die y-Achse und der Vektor 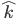 die z-Achse. In der Welt der Quantenmechanik gibt es ebenfalls die genannte 3 Achsen. Bevor wir diese jedoch definieren ist es nochmals wichtig zu wiederholen, dass eine Messung des Spins stets diskret stattfindet. Wir könnten fragen: Zeigt der Spin in diese Richtung? Die Messung wird entweder "Der Spin zeigt in diese Richtung" oder "Der Spin zeigt exakt in die andere Richtung" zurückgeben. Insofern wir die Messungen auf die genannten 3 Achsen beschränken, so bedeutet dies für uns, dass wir unsere Messungen auf folgende 3 Fragestellungen reduzieren können:
die z-Achse. In der Welt der Quantenmechanik gibt es ebenfalls die genannte 3 Achsen. Bevor wir diese jedoch definieren ist es nochmals wichtig zu wiederholen, dass eine Messung des Spins stets diskret stattfindet. Wir könnten fragen: Zeigt der Spin in diese Richtung? Die Messung wird entweder "Der Spin zeigt in diese Richtung" oder "Der Spin zeigt exakt in die andere Richtung" zurückgeben. Insofern wir die Messungen auf die genannten 3 Achsen beschränken, so bedeutet dies für uns, dass wir unsere Messungen auf folgende 3 Fragestellungen reduzieren können:
- Zeigt der Spin des Elektrons entlang ("spin up") oder entgegen ("spin down") der X-Achse?
- Zeigt der Spin des Elektrons entlang ("spin up") oder entgegen ("spin down") der Y-Achse?
- Zeigt der Spin des Elektrons entlang ("spin up") oder entgegen ("spin down") der Z-Achse?
Daraus resultieren für uns zwei Fragestellungen:
- Wie wird der Zustand des Spins eines Elektrons mathematisch beschrieben?
- Wie wird der Zustand des Spins eines Elektrons gemessen?
Wichtig an dieser Stelle: Es muss kein Elektron sein. Wir werden in Zukunft einen etwas generischeren Begriff verwenden - das Qubit. Wikipedia hat eine schöne Definition eines Qubits: "Ein Qubit [..] ist ein System, das nur durch die Quantenmechanik korrekt beschrieben wird und das nur zwei, durch Messung sicher unterscheidbare Zustände hat".[3]
(Der Richtigkeit halber ein Hinweis: Wir werden im Folgenden mit Spin 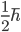 Teilchen rechnen, also z.B. dem Spin eines Elektrons.)
Teilchen rechnen, also z.B. dem Spin eines Elektrons.)
Kapitel 6: Das Qubit
Waren in einem 3-dimensionalen Raum drei Basis-Vektoren zur Beschreibung des Vektors notwendig (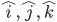 ), so sind in einem zweidimensionalen Quantensystem zwei Basis-Vektoren notwendig: Ein Vektor, der beschreibt, dass anhand einer Achse (z.B. der z-Achse) das Qubit parallel ("spin up") verläuft, ein zweiter für die exakt gegenläufige ("antiparallele") Richtung ("spin down").
), so sind in einem zweidimensionalen Quantensystem zwei Basis-Vektoren notwendig: Ein Vektor, der beschreibt, dass anhand einer Achse (z.B. der z-Achse) das Qubit parallel ("spin up") verläuft, ein zweiter für die exakt gegenläufige ("antiparallele") Richtung ("spin down").
Ein bildliches Beispiel: Die z-Achse in einem dreidimensionalen Raum ist die Achse, die nach oben bzw. unten zeigt. Insofern der Spin eines Qubits nach "oben" zeigt, nennt man die Richtung "spin up". Zeigt der Spin eines Qubits nach "unten", so wird die Richtung "spin down" genannt.
Die genannte Erklärung wird in folgender Gleichung dargestellt:
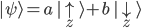
Nicht erschrecken, es ist eigentlich ganz einfach: Das erste Symbol 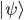 bezeichnet einfach nur ein Qubit.
bezeichnet einfach nur ein Qubit. 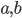 sind komplexe Zahlen, daher gilt:
sind komplexe Zahlen, daher gilt: 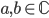 . Die komplexe Zahlen sind, wenn sie ins Quadrat genommen werden, die Wahrscheinlichkeiten, das dahinterliegende Ergebnis bei einer Massung zu erhalten. Die Symbole
. Die komplexe Zahlen sind, wenn sie ins Quadrat genommen werden, die Wahrscheinlichkeiten, das dahinterliegende Ergebnis bei einer Massung zu erhalten. Die Symbole 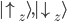 stehen stellvertretend für "spin up" und "spin down" in Bezug auf die z-Achse.
stehen stellvertretend für "spin up" und "spin down" in Bezug auf die z-Achse.
Ein Beispiel:
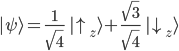
Da die Spin up/ Spin down Symbole in Bezug auf die z-Achse definiert wurden, ist die Wahrscheinlichkeit, dass das Qubit bei einer Messung "spin up" bzw "spin down" zurückgibt wie folgt:
Die Wahrscheinlichkeit für 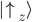 ist:
ist: 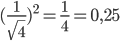
Die Wahrscheinlichkeit für 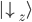 ist:
ist: 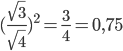
Die Summe der quadrierten komplexen Zahlen 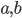 muss stets 1 ergeben. Wir können dies an unserem Beispiel-Qubit testen:
muss stets 1 ergeben. Wir können dies an unserem Beispiel-Qubit testen:
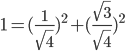
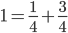
In unserem Fall war die obere Formel somit korrekt.
Kapitel 7: Messungen
In einem vorherigen Kapitel haben wir bereits über das Skalarprodukt gesprochen. Es hat rechnerisch gezeigt, wie sehr, vereinfacht gesagt, zwei Vektoren in die gleiche Richtung zeigen. In der Welt der Quantenphysik gibt es das ebenfalls, dort wird es auf englisch das Inner Product genannt.
Ein Beispiel: Wir haben den Vektoren 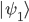 sowie den Vektor
sowie den Vektor 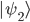 . Diese sind wie folgt deklariert:
. Diese sind wie folgt deklariert:
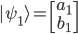
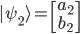
Wir möchten jetzt feststellen, inwiefern die beiden Vektoren in dieselbe Richtung zeigen. Bei einem klassischen Vektor hätten wir jetzt 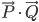 gerechnet. In der Quantenmechanik gestaltet sich die Rechnung identisch:
gerechnet. In der Quantenmechanik gestaltet sich die Rechnung identisch:
Das Inner Product ist: 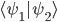
Anders formuliert: Das bra 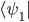 wird mit dem ket
wird mit dem ket 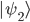 multipliziert.
multipliziert.
Vorab stellt sich hier die Frage: Wie können wir das bra 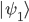 in das ket
in das ket 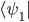 umwandelt? Hierzu müssen wir den Inhalt des ersten Vektors komplex konjugieren (siehe Kapitel 1). Im konkreten Beispiel ergibt sich daher die folgende Rechnung:
umwandelt? Hierzu müssen wir den Inhalt des ersten Vektors komplex konjugieren (siehe Kapitel 1). Im konkreten Beispiel ergibt sich daher die folgende Rechnung:
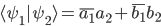
Ein kleiner Hinweis in Bezug auf die Rechnung mit komplexen Zahlen:
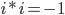
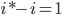
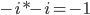
In einem späteren Beispiel werden die Umrechnung sowie das Inner Product nochmals verdeutlichen.
Kapitel 8: Die Orthonormalbasis
Zum Verständnis der Grundlagen fehlt uns aktuell noch ein Puzzleteil: Was verbirgt sich eigentlich hinter den Basisvektoren wie 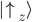 ?
?
Das Wort Orthonormalbasis definiert Wikipedia wie folgt: "Eine Orthonormalbasis [..] ist eine Menge von Vektoren aus einem Vektorraum mit Skalarprodukt (Innenproduktraum), welche auf die Länge 1 normiert und zueinander orthogonal [...] liegen". [5] Anders ausgedrückt: Eine Orthonormalbasis besteht aus Einheitsvektoren die zueinander das Skalarprodukt null haben, d.h. alle im rechten Winkel zueinander stehen.
Auf einem "klassisch-dreidimensionalen" Koordinatensystem wäre die Orthonormalbasis z.B.:
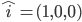
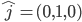
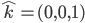
Das kommt uns bekannt vor 🙂 Eben diese rechtwinklig ("orthogonal") zueinander stehenden Vektoren gibt es auch in der Quantenmechanik - dort sind jedoch, durch die komplexen Zahlen, (im Falle von Spin 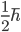 Teilchen) zwei Vektoren für ein dreidimensionales System ausreichend. Spätestens an diesem Punkt nochmals der Hinweis: Bitte übertragt die folgenden Vektoren nicht in ein klassisches Koordinatensystem.
Teilchen) zwei Vektoren für ein dreidimensionales System ausreichend. Spätestens an diesem Punkt nochmals der Hinweis: Bitte übertragt die folgenden Vektoren nicht in ein klassisches Koordinatensystem.
In der Quantenmechanik wird die x-Achse wird beschrieben durch
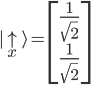 und
und 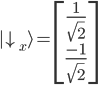
Die y-Achse wird beschrieben durch
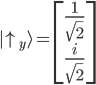 und
und 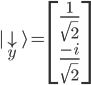
Die z-Achse wird beschrieben durch
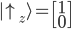 und
und 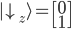
Eine bildliche Darstellung für die Orthonormalbasis wäre das Messgerät aus dem letzten Artikel. Möchten wir, wie im letzten Artikel getan, das Messgerät drehen, so ändern wir mathematisch vereinfacht gesagt die Orthonormalbasis. Im konkreten Beispiel haben wir das Messgerät z.B. von der x-Achse auf die y-Achse gedreht. Für eine Orthonormalbasis müssen grundsätzlich zwei Einheitsvektoren im rechten Winkel zueinander stehen, d.h. 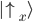 und
und 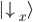 ,
,  und
und 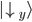 oder
oder 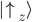 und
und 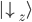 .
.
Kapitel 9: Ein konkretes Beispiel
Als Grundlage soll das bisher vermittelte Wissen ausreichen. Zeit für eine Zusammenfassung. Am Besten lässt sich das bisher gelernte an einem konkreten Beispiel erklären.
Gegeben sei folgender State:
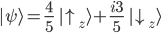
Im Folgenden werden wir das Qubit auf Basis der x, y und z-Achse mathematisch bestimmen, daher die Wahrscheinlichkeiten für ein jeweiliges Messergebnis "spin up" oder "spin down" ermitteln.
1. Wie hoch ist die Wahrscheinlichkeit für ein "spin up" in Bezug auf die x-Achse?
Ein "spin up" auf der x-Achse wurde im Kapitel 8 mit folgendem Vektor beschrieben:
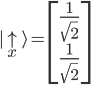
Wir ermitteln nun die Wahrscheinlichkeit mit dem inneren Produkt (Skalarprodukt) im Quadrat, d.h. wie sehr unser Vektor 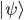 in dieselbe Richtung des Vektors
in dieselbe Richtung des Vektors 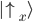 zeigt:
zeigt:
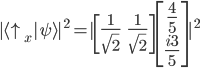
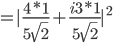
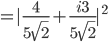
Bei 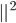 wird nur der absolute Teil von
wird nur der absolute Teil von 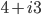 quadriert:
quadriert:
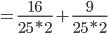
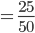
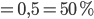
Die Wahrscheinlichkeit für ein "spin up" in Bezug auf die x-Achse liegt bei 50%.
2. Wie hoch ist die Wahrscheinlichkeit für ein "spin down" in Bezug auf die x-Achse?
Ein "spin down" auf der x-Achse wurde im Kapitel 8 mit folgendem Vektor beschrieben:
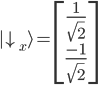
Wir ermitteln nun die Wahrscheinlichkeit mit dem inneren Produkt (Skalarprodukt) im Quadrat, d.h. wie sehr unser Vektor 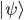 in dieselbe Richtung des Vektors
in dieselbe Richtung des Vektors 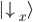 zeigt:
zeigt:
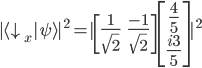
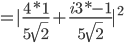
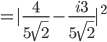
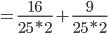
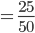
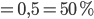
Die Wahrscheinlichkeit für ein "spin down" in Bezug auf die x-Achse liegt bei 50%.
3. Wie hoch ist die Wahrscheinlichkeit für ein "spin up" in Bezug auf die y-Achse?
Ein "spin up" auf der y-Achse wurde im Kapitel 8 mit folgendem Vektor beschrieben:
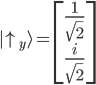
Wir ermitteln nun die Wahrscheinlichkeit mit dem inneren Produkt (Skalarprodukt) im Quadrat, d.h. wie sehr unser Vektor 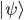 in dieselbe Richtung des Vektors
in dieselbe Richtung des Vektors  zeigt:
zeigt:
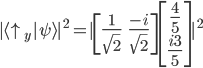
Durch die komplexen Konjugation wurde aus der Zahl 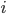 ein
ein 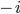 im bra.
im bra.
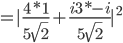
Wie oben beschrieben: 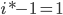
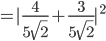
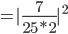
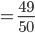
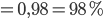
Die Wahrscheinlichkeit für ein "spin up" in Bezug auf die y-Achse liegt bei 98%.
4. Wie hoch ist die Wahrscheinlichkeit für ein "spin down" in Bezug auf die y-Achse?
Ein "spin down" auf der y-Achse wurde im Kapitel 8 mit folgendem Vektor beschrieben:
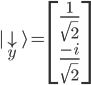
Wir ermitteln nun die Wahrscheinlichkeit mit dem inneren Produkt (Skalarprodukt) im Quadrat, d.h. wie sehr unser Vektor 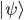 in dieselbe Richtung des Vektors
in dieselbe Richtung des Vektors 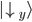 zeigt:
zeigt:
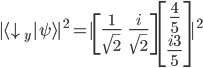
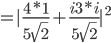
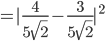
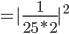
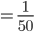
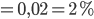
Die Wahrscheinlichkeit für ein "spin down" in Bezug auf die y-Achse liegt bei 2%.
5. Wie hoch ist die Wahrscheinlichkeit für ein "spin up" in Bezug auf die z-Achse?
Eigentlich ist dieser Rechnung nicht notwendig, da das Ergebnis direkt aus der oberen Gleichung abgelesen werden kann. Der Vollständig dienend dennoch die Rechnung: Ein "spin up" auf der z-Achse wurde im Kapitel 8 mit folgendem Vektor beschrieben:
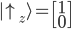
Wir ermitteln nun die Wahrscheinlichkeit mit dem inneren Produkt (Skalarprodukt) im Quadrat, d.h. wie sehr unser Vektor 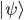 in dieselbe Richtung des Vektors
in dieselbe Richtung des Vektors 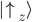 zeigt:
zeigt:
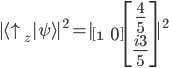
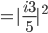
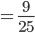
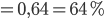
Die Wahrscheinlichkeit für ein "spin up" in Bezug auf die z-Achse liegt bei 64%.
6. Wie hoch ist die Wahrscheinlichkeit für ein "spin down" in Bezug auf die z-Achse?
Ein "spin down" auf der z-Achse wurde im Kapitel 8 mit folgendem Vektor beschrieben:
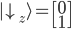
Wir ermitteln nun die Wahrscheinlichkeit mit dem inneren Produkt (Skalarprodukt) im Quadrat, d.h. wie sehr unser Vektor 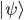 in dieselbe Richtung des Vektors
in dieselbe Richtung des Vektors 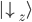 zeigt:
zeigt:
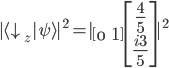
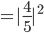
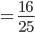
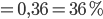
Die Wahrscheinlichkeit für ein "spin down" in Bezug auf die z-Achse liegt bei 36%.
Die mathematischen Grundlagen sind gelegt - im nächsten Beitrag werden wir uns eine "unknackbare" quantenkryptographische Schlüsselaustauschfunktion anschauen - ein spannendes Thema der Quantenkryptographie!
Quellen / Bildnachweis:
- Beitragsbild: © Peter Jurik/stock.adobe.com
- [1] Yomomo / CC BY-SA
- [2] Nobel Foundation / Public domain
- [3] Wikipedia (de): Qubit; abgerufen am 14.04.2020 unter https://de.wikipedia.org/wiki/Qubit
- [4] Alva2004 / CC BY-SA
- [5] Wikipedia (de): Orthonormalbasis; abgerufen am 20.04.2020 unter https://de.wikipedia.org/wiki/Orthonormalbasis

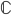
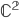
alter Schwede….
Danke!