Im dritten Beitrag meiner Reihe "Quantencomputing und Quantenkryptographie einfach erklärt" werde ich ein Hauptthema der Quantenkryptographie näher erläutern: Quantenschlüsselaustauschprotokolle, im Detail das Protokoll BB84. Klingt kompliziert, aber keine Angst - bevor wir uns das Protokoll näher anschauen, werden wir uns vorab erst einmal mit dem Sinn und Zweck von solchen Protokollen im Allgemeinen beschäftigen und dies völlig unabhängig von der Quantenkryptographie. Hierbei werden wir recht schnell erkennen, dass Schlüsselaustauschprotokolle alltäglich im Einsatz sind - auch in den Moment, in dem Du diese Webseite geöffnet hast.
Vorab der übliche Disclaimer: Ich bin weder Mathematiker, noch Physiker. Aus diesem Grund werde ich sicherlich nicht alle Punkte mit mathematisch/ physischer Präzision korrekt formuliert darlegen können. Insofern du Verbesserungsvorschläge für die Beiträge hast, so freue ich mich selbstverständlich über einen Kommentar oder Feedback.
| Dieser Artikel ist Teil einer Serie:
- Teil 1: Was ist Spin? |
Kapitel 1: Grundlagen Verschlüsselung
Beginnen werde ich dieses Mal mit einer Problembeschreibung, die völlig unabhängig von der Quantenkryptographie ist: Wie können zwei oder mehr Personen sicher miteinander kommunizieren? In meinen Kursen habe ich zur Darstellung des Problems sehr gerne das folgende Szenario genommen: Wir stellen uns für einen Moment vor, dass wir uns mitten auf einer belebten Kreuzung befinden, beispielsweise hier:

Die Aufgabenstellung: Wie können die beiden rot markierten Person eine Nachricht austauschen, ohne dass diese sich näher kommen dürfen? Natürlich sind wir in einer modernen Welt, Smartphones existieren bereits. Aber wie stellt beispielsweise ein Smartphone sicher, dass eine Nachricht unverändert und vertraulich beim Empfänger ankommt?
Um das Problem nicht unnötig kompliziert zu machen, gibt es eine weitere Vereinfachung: Die beiden Personen sollen eine Nachricht ganz ohne IT austauschen - mit Zettel und Stift. Im Klartext wäre das ziemlich einfach: Eine Person schreibt eine Nachricht, anschließend wird der Zettel einfach von Person zu Person durchgereicht bis dieser beim Empfänger angekommen ist.

Die Darstellung ist von der Realität übrigens gar nicht so weit entfernt. Bevor beispielsweise eine Whatsapp-Nachricht beim Empfänger ankommt, können ziemlich viele Unternehmen und Personen an der Zustellung beteiligt sein. Am Bild sehen wir schon das Problem: So richtig sicher ist das Ganze leider nicht. Ich habe keine Garantie, dass die Nachricht unterwegs vertraulich behandelt wird und unverfälscht beim Empfänger ankommt. Auch das ist ziemlich nah an der digitalen Realität.
Wie können wir das Problem lösen?
Die erste Antwort, die hier meist sehr schnell von meinen Teilnehmern kam war: Verschlüsselung! Letztendlich die Modifikation der Nachricht mit Hilfe irgendeiner Methodik um die Lesbarkeit zu erschweren. Beispielsweise durch den Austausch von Buchstaben durch andere Buchstaben oder durch aktuelle Verfahren, wie beispielsweise AES. Hierbei handelt es sich um Methoden, die zur Ver- und Entschlüsselung einen vorab vereinbarten Schlüssel benötigen, die so genannten symmetrischen Verschlüsselungsverfahren.
Löst das unser Problem? Leider nur auf den ersten Blick. Ein entscheidendes Problem bleibt: Wie können die beiden Gesprächspartner einen sicheren Schlüssel miteinander austauschen? Ohne gemeinsames Passwort haben wir das Problem, dass Bob keine Möglichkeit hätte, eine von Alice verschlüsselte Nachricht zu entschlüsseln - denn mit welchem Schlüssel soll Bob das auch tun? Das Problem wird, leider, häufig auch in Unternehmen wie folgt gelöst: Eine wichtige Nachricht wird beispielsweise mit 7-ZIP verschlüsselt und per E-Mail versendet. Das Passwort selbst wird in einer separaten E-Mail hinterher gesendet. Wo ist das Problem?

Ich denke, die Darstellung ist eindeutig. Hat jemand die Möglichkeit, die E-Mails unterwegs abzufangen, so hat er auch die Möglichkeit, das Passwort abzufangen. Gleiches gilt in der anlogen Welt: Sendet Alice ihr zufälliges Passwort auf einem getrennten Zettel zu Bob, so ist die Sicherheit nicht gegeben. Wer die erste Nachricht abfangen könnte, der kann auch die Zweite abfangen.
Kapitel 2: Schlüsselaustauschprotokolle
Zur Lösung exakt dieses Problems wurden Schlüsselaustauschprotokolle, auf englisch Key-Exchange-Protocols, entwickelt. Schlüsselaustauschprotokolle stellen sicher, das Alice und Bob auf sichere Art und Weise ein gemeinsames Passwort aushandeln können. Das ausgehandelte Passwort wird anschließend genutzt, um die Nachricht selbst mit einem Verfahren wie z.B. AES zu verschlüsseln.
Wer bisher schon einmal etwas mit Verschlüsselung zu tun gehabt hat, hat sicher bereits etwas von Public-Key oder asymmetrischer Verschlüsselung gehört. Kurz beschrieben: Alice generiert mathematisch ein Schlüsselpaar, dass aus einem privaten und einem öffentlichen Schlüssel besteht. Die Schlüssel unterscheiden sich, der öffentliche Schlüssel kann zur Verschlüsselung, aber nur der private Schlüssel zur Entschlüsselung genutzt werden. Der private Schlüssel bleibt bei Alice, der öffentliche Schlüssel wird an Bob übergeben. Somit kann Bob eine Nachricht mit dem öffentlichen Schlüssel von Alice verschlüsseln und die verschlüsselte Nachricht an Alice senden. Anschließend kann ausschließlich Alice mit ihrem privaten Schlüssel die Nachricht von Bob wieder entschlüsseln. Genau so funktioniert übrigens E-Mailverschlüsselung mit PGP, S/MIME oder auch z.B. der Messenger Threema. Die genutzten Verfahren sind z.B. unter dem Namen RSA oder Elliptic Curve Cryptography (ECC) bekannt. Auch Webseiten, die über eine verschlüsselte Verbindung (TLS => https) arbeiten, funktionieren teilweise noch nach diesem Verfahren, glücklicherweise jedoch immer weniger.
Das Verfahren hat einige große Nachteile:
- Nachteil 1: Ein Angreifer, der in der Lage ist, alle verschlüsselt ausgetauschten Nachrichten mitlesen und speichern zu können, der kann, insofern er zu einem späteren Zeitpunkt an den privaten Schlüssel kommt, nachträglich alle in der Vergangenheit gesendeten Nachrichten entschlüsseln. Technisch ausgedrückt: asymmetrische Verschlüsselungen, wie RSA oder ECC, bieten kein Perfect Forward Secrecy (PFS).
- Nachteil 2: Ein weiteres Problem, dass jedoch nicht auf asymmetrische Verfahren beschränkt ist: Wie kann Bob sichergehen, dass er den korrekten Schlüssel von Alice erhalten hat? Kann Bob sichergehen, dass der öffentliche Schlüssel nicht durch jemanden ("Man in the Middle") ausgetauscht wurde?
Der erste Nachteil wurde gelöst, erstmalig im breiten Einsatz durch den Diffie-Hellman-Schlüsselaustausch. Kurz zur Funktionsweise: Das Protokoll ermöglicht folgende Szenario:

Alice und Bob stehen wieder auf der bekannten Kreuzung und haben eine so laute Stimme, dass sie sich gegenseitig etwas zurufen können. Das Ganze jedoch im Klartext, also für jeden anderen auf der Kreuzung hörbar. Im Rahmen des Diffie-Hellman-Schlüsselaustausches müssen Alice und Bob einige Informationen austauschen, zum Beispiel durch lautes zurufen. Auch wenn jeder andere auf der Kreuzung alles mitgehört hat, so ermöglicht es der Diffie-Hellman-Schlüsselaustausch durch etwas Mathematik auf ein Geheimnis kommen, welches nur Alice und Bob bekannt ist. Klingt erstmal etwas unwirklich, funktioniert mathematisch jedoch ziemlich einfach. Letztendlich ermöglicht es auch das, was im breiten Sprachgebrauch unter Perfect Forward Secrecy (PFS) verstanden wird: Für jede Verbindung wird ein individueller Schlüssel vereinbart. Somit ist es nicht mehr möglich, dass ein Angreifer alle ausgetauschten Nachrichten einfach speichert und darauf hofft, eventuell später an den privaten Key zu gelangen.
Wir halten fest: Schlüsselaustauschprotokolle ermöglichen es zwei Gesprächspartnern einen gemeinsamen geheimen Schlüssel (das "Passwort") zur vereinbaren. Der Schlüssel kann anschließend dazu genutzt werden, symmetrische Verfahren wie z.B. AES zum Einsatz zu bringen.
Kapitel 3: Was ist eigentlich Quantenkryptographie?
Der erste Beitrag ist direkt in die Quantenmechanik und Spin eingestiegen, der zweite Beitrag dieser Reihe hat einige mathematische Grundlagen gelegt. Offen gelassen habe ich die Frage: Was wird eigentlich unter Quantenkryptographie verstanden?
Kurze Antwort: Kryptographische Verfahren unter dem Einsatz quantenmechanischer Effekte.
Etwas detaillierter: Momentan wird darunter insbesondere ein Schlüsselaustauschprotokoll unter Nutzung quantenmechanischer Effekte verstanden. Es handelt sich somit um eine Alternative zum gerade beschriebenen Diffie-Hellman-Schlüsselaustausch. Daneben gibt es noch weitere Themenbereiche der Quantenkryptographie, beispielsweise Algorithmen, die einige aktuelle Verfahren brechen könnten, hierzu jedoch erst zu einem späteren Zeitpunkt mehr.
Das Wissen aus den ersten beiden Beiträgen reicht übrigens völlig aus, um die Funktionsweise des Quanten-Schlüsselaustauschprotokolls BB84 zu verstehen. Wichtig ist es jedoch, sich nochmals folgende Eigenheiten der Quantenmechanik zu verinnerlichen:
- Messungen in der Welt der Quantenphysik sind diskret: Es gibt nur 2 mögliche Antworten einer Messung.
- Messungen beeinflussen das Messobjekt: Das Ergebnis der Messung ist der neue Zustand des Messobjekts. Es ist nach einer Messung nicht mehr möglich, den alten Zustand wiederherzustellen.
- Wird entlang einer Achse, z.B. der X-Achse gemessen, so ist die darauffolgende Messung anhand der Y oder Z Achse stets mit zufälligem (50/50) Ausgang.
Um auch die Mathematik des letzten Beitrags wieder etwas aufzufrischen, ein Beispiel:
Gegeben sei folgender Zustand:
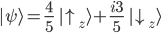
Insofern wir jetzt eine Messung durchführen, so kollabiert die Funktion auf das gemessene Ergebnis. Haben wir beispielsweise "Spin up" gemessen, so wäre der Zustand nach der Messung:
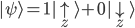
Eine erneute Messung führt somit mit 100% Wahrscheinlichkeit erneut zu einem "Spin up". Ein State "Spin up entlang der z-Achse" erzeugt bei einer nachfolgenden Messung auf der x- und y-Achse eine 50/50 Wahrscheinlichkeit:
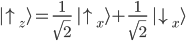
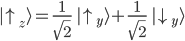
Nicht vergessen: Um die Wahrscheinlichkeit zu erhalten müssen die komplexe Zahlen quadriert werden. Im Beispiel:
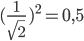
Mit dem Wissen der ersten beiden Kapitel sind wir gut gerüstet - Jetzt wird es Zeit dem Quanten-Schlüsselaustauschprotokoll BB84 näher zu kommen.
Kapitel 4: Photonen und ihre Polarisierung
Bisher haben wir mit Elektronen und ihrem Spin gearbeitet. Die genannten Effekte treten jedoch auch bei weiteren Teilchen auf, beispielsweise bei Photonen. Was bei Elektronen der Spin ist, ist bei Photonen die Polarisierung. Die Möglichkeiten polarisierten Lichts werden manche beispielsweise aus einem 3D-Kino oder aus der Fotographie kennen.
Über eine Lichtquelle wird ein Polarisationsfilter gelegt, also ein Filter, der beispielsweise ausschließlich horizontal polarisiertes Licht durchlässt. Wird darüber ein weiterer Filter gelegt, der ebenfalls horizontal polarisiertes Licht durchlässt, so wird sich das Ergebnis nicht ändern:

Soweit nicht weiter spannend. Wir machen nun das gleiche Experiment, jedoch mit einem horizontal und einem vertikal polarisierten Filter:

In diesem Fall hat der Filter sämtliches Licht absorbiert - horizontal polarisiertes Licht durchdringt keinen vertikalen Filter. Nun ein weiteres Experiment: Was passiert, wenn wir zwei horizontale Filter in einem 45° Winkel übereinander legen?

Was ist passiert? Genau 50% des Lichts passieren den zweiten Filter. 50/50 - eine Wahrscheinlichkeit, die wir auch beim Elektronen-Spin kennengelernt haben.
Ändern Polarisationsfilter die Polarisierung des Lichts oder filtern sie dieses nur aus? Anders gesagt: Beeinflusst die Messung den Zustand des Photons? Auch dies lässt sich experimentell ziemlich einfach nachweisen. Wir nehmen das Experiment, in welchem ein vertikaler über einen horizontalen Filter gelegt wurde und passen dieses an. Bisher haben die beiden Filter 100% des Lichts absorbiert. In einem neuen Experiment werden wir nun einen weiteren 45 Grad gedrehten Filter zwischen die beiden Filtern schieben:

Das Experiment zeigt es sehr deutlich - die Filter polarisieren das Licht neu. In Summe ermöglichen uns Photonen ähnliche Eigenschaften, die wir bisher bei Elektronen kennengelernt haben:
- Messungen in der Welt der Quantenphysik sind diskret: Entweder das Photon geht durch den Filter durch oder es wird gefiltert.
- Messungen beeinflussen das Messobjekt: Eine Messung mit einem Filter verändert die Polarisierung des Photons.
- Wird über einem Filter ein 45 Grad gedrehter Filter gelegt, so ist die darauffolgende Messung stets mit zufälligem (50/50) Ausgang.
Photonen haben im Gegensatz zu Elektronen einen entscheidenden Vorteil: Der Zustand eines Photons ("die Polarisierung") kann über eine lange Distanz aufrecht erhalten werden. Den Zustand eines Elektrons ("der Spin") über eine lange Distanz aufrecht zu halten, ist erheblich komplizierter.
Kapitel 5: Der BB84 Versuchsaufbau
Das Ziel des Experiments ist es, dass Alice und Bob einen sicheren, gemeinsamen Schlüssel ausgetauschen können. Das BB84-Protokoll ist aus dem Jahr 1984 und nach seinen Erfindern Charles Bennett und Gilles Brassard benannt. Der Aufbau des Experiments gestaltet sich wie folgt:

Alice sendet zufällig polarisierte Photonen an Bob. Die Photonen können 45 Grad polarisiert (im Bild schwarz), -45 Grad polarisiert (orange), 0 Grad polarisiert/ vertikal (grün) oder 90 Grad polarisiert/ horizontal (blau) sein. Die Polarisierung passiert völlig zufällig und wird von Alice protokolliert, jedoch noch nicht Bob mitgeteilt.
Eine Messung in der Quantenmechanik kann nur diskret stattfinden: Wir könnten beispielsweise prüfen, ob ein Photon vertikal polarisiert ist und bekommen als Antwort ein einfaches Ja (=ist vertikal) oder ein Nein (=ist horizontal). Bob muss sich jedoch vor der Messung überlegen, ob er das Photon 0°/90° oder -45°/+45° misst. Die Messung selbst legt den Zustand fest - nach einer Messung befindet sich das Photon mit 100% Wahrscheinlichkeit im gemessenen Zustand. Da Bob keine Ahnung hat, wie ein einkommendes Photon polarisiert sein wird entscheidet sich Bob völlig zufällig, mit welcher Basis Bob das nächste Photon messen wird. Bob notiert sich anschließend das Ergebnis gemeinsam mit der jeweils verwendeten Basis.
Kapitel 6: Ein Zwischenergebnis
Nach Durchführung des Experiments haben sowohl Alice als auch Bob voneinander getrennte Aufzeichnungen. Alice hat beispielsweise folgende Aufzeichnungen vorgenommen:
| Code | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| Photon | 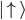 |
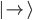 |
 |
 |
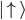 |
 |
 |
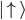 |
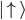 |
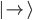 |
Bob könnte zeitgleich die folgenden Aufzeichnungen vorgenommen.
| Basis | 0° | 0° | 45° | 0° | 45° | 45° | 0° | 45° | 0° | 45° |
| Result | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Was Bob zu diesem Zeitpunkt noch nicht weiß: Die roten Ergebnisse sind völlig zufällig. In diesem Fall wurde ein eintreffendes Photon zufällig mit der falschen Basis gemessen. In diesem Fall ist das Ergebnis 50/50.
Kapitel 7: Der Schlüssel wird berechnet
Nachdem jede Partei ihr Ergebnis notiert hat, übersendet Alice über eine authentifizierte Leitung an Bob eine Liste der jeweils verwendeten Basis (0/90 Grad vs. -45/45 Grad). Im Beispiel könnte dies wie folgt aussehen:
| Alice | 0° | 0° | 45° | 45° | 0° | 45° | 45° | 0° | 0° | 0° |
Bob vergleich diese Liste mit seinen Ergebnissen. Er streicht hierbei alle Einträge aus der Liste, die nicht mit seiner zufällig gewählten Basis übereinsteimmen:
| Alice | 0° | 0° | 45° | 45° | 0° | 45° | 45° | 0° | 0° | 0° |
| Basis | 0° | 0° | 45° | 0° | 45° | 45° | 0° | 45° | 0° | 45° |
| Result | 1 | 0 | 1 | 0 | 1 |
Bob teilt Alice anschließend über eine authentifizierte Leitung mit, welche Photonen er gestrichen hat. Im Beispiel wäre es Eintrag Nr. 4, 5, 7, 8, 10 und 11. Rein statistisch werden auf lange Dauer die Hälfte der Einträge übrig bleiben. Das daraus resultierende Passwort wäre 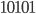 .
.
Kapitel 8: Man-in-the-Middle Angriff
Die schönste Erklärung kryptographischer Protokolle wäre langweilig, wenn nicht auch ein Angreifer, hier genannt Eve, auf der Bildfläche erscheinen würde. Wir nehmen das folgende Szenario an: Eve befindet sich zwischen Alice und Bob und misst die Photonen, die Alice an Bob versendet. Nach der Messung sendet Eve die Photonen an Bob weiter. Eine Messung eines Photons führt grundsätzliche dazu, dass das Messergebnis den Zustand des Messobjekts festlegt. Insofern Eve zufällig ein Photon entlang der Polarisation misst, in welcher Alice es versendet hat, so würde Bob nichts vom Angriff bemerken. Insofern Eve jedoch die Polarisierung ändert, so hätte Bob mit einer Wahrscheinlichkeit von 50% ein falsches Messergebnis. Insofern Eve eine zufällige Messbasis wählt, so können wir davon ausgehen, dass im Mittel 25 Prozent aller Messungen fehlerhaft sein werden. Zur Prüfung würde ein statistischer Test ausreichen: Alice und Bob könnten einige Bits über den unsicheren Kanal vergleichen. Ist die Fehlerrate zu hoch, so kann von einem Angriff ausgegangen werden. In der Praxis könnte die Fehlerrate natürlich auch zahlreiche andere Ursachen beispielsweise technischer Art haben.
An dieser Stelle möchte ich einen wichtigen Begriff kurz erläutern: Das No-Cloning-Theorem. Das No-Cloning-Theorem sagt aus, dass es nicht möglich ist ein beliebiges Qubit zu kopieren, ohne dabei das originale Qubit zu verändern. In der Quantenmechanik ist es nicht möglich, eine Kopie eine perfekte Kopie eines Qubits zu erzeugen.[2]
Quellen / Bildnachweis:
- Beitragsbild: © Peter Jurik/stock.adobe.com
- [1] Ryoji Iwata/usplash.com
- [2] Siehe auch: Wikipedia: Das No-Cloning-Theorem
