Nachdem es relativ wenig Beiträge gibt, die die Grundlagen des Quantencomputings bzw. der Quantenkryptographie einfach verständlich erklären, möchte ich im Folgenden mit einer Beitragsreihe das Themenfeld erklären. Vorab: Ich bin weder Mathematiker, noch Physiker, was vielleicht auch ein Vorteil sein kann, wenn man komplexe Sachverhalte aus den genannten Themengebieten einfach erklären möchte. Sicherlich werde ich nicht alle Punkte mit mathematisch/ physischer Präzision korrekt formuliert darlegen können - was für ein Grundverständnis jedoch auch nicht notwendig ist.
| Dieser Artikel ist Teil einer Serie:
- Teil 1: Was ist Spin? |
Insofern du Verbesserungsvorschläge für die Beiträge hast, so freue ich mich selbstverständlich über einen Kommentar oder Feedback. Letztendlich ist es ein Thema, welches mich selbst seit einigen Monaten sehr interessiert - und es gibt keinen Weg, etwas besser zu lernen, als es selbst für andere verständlich aufzubereiten. Natürlich werde ich den Fokus auf die relevanten IT-Security Themen aus dem Bereich nicht aussparen.
Kapitel 1: Der Einstieg
Ich habe in den letzten Monaten relativ viele Bücher zum Thema gelesen, eins hatten fast alle gemeinsam: den Einsteig ins Thema. Als guter Einstieg wird oftmals das Stern-Gerlach Experiment verwendet. Im Februar 1922 wurden von Otto Stern und Walther Gerlach erstmals bestimmte für uns im Folgenden relevante Eigenschaften anhand von Silberatomen experimentell bestätigt.

Aber der Reihe nach: Bevor ich das Experiment selbst erklären möchte, müssen wir auf eine Besonderheit bei Silberatomen eingehen - denn genau diese wurden im Experiment von Gerlach-Stern verwendet.
Im Bohrsches Atommodell von 1922 beschreibt Niels Bohr sein Verständnis von Atomen - ein Modell, das einige sicherlich noch aus der Schulzeit kennen könnten.

In seinem Modell halten sich Elektronen auf Kreisbahnen um den Atomkern herum auf. Im Falle des chemischen Elements Silber (Ag) sind dies 47 Elektronen. Von diesen sind 2 Elektronen im innersten Orbit, 8 Elektronen im Zweiten und jeweils 18 Elektronen im dritten und vierten Orbit. Das letzte Elektron, also das 47., befindet sich alleine auf dem äußersten Orbit. Graphisch vereinfacht dargestellt sieht Silber im genannten Atommodell wie folgt aus:
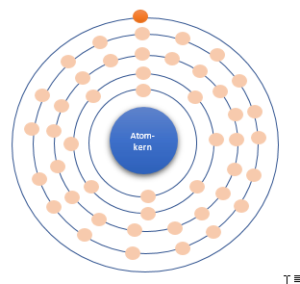
Zirkulierende Elektronen generieren ein Magnetfeld - in den inneren Schalen sind diese jedoch immer in gegenläufigen Zweier-Pärchen, sodass sich das durch sie erzeugte Magnetfeld aufhebt. Diese Elektronen habe ich mit einem hellen Orange markiert. Das für uns relevante Elektron ist das Elektron im dunklen Orange - dieses erzeugt ein Magnetfeld, welches nicht durch ein zweites Elektron aufgehoben wird. Letztendlich ist das äußerste Elektron maßgeblich für das magnetische Feld des Silberatoms verantwortlich.
Kapitel 2: Das Stern-Gerlach Experiment
Das Stern-Gerlach Experiment hat weitere Details über das Magnetfeld von Silberatomen herausgefunden. Hierbei ging es unter anderem um die Frage, inwiefern die Nord-Süd Achse des Silberatom-Magnetfelds angeordnet ist. Als Versuchsaufbau diente, vereinfacht darstellt, das folgende Setting:
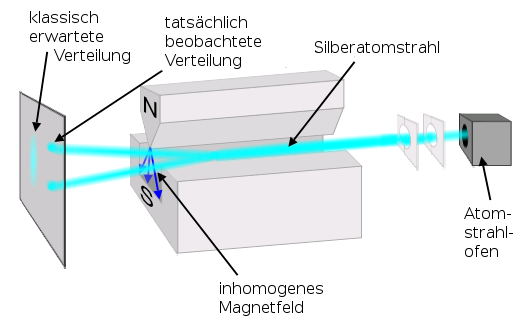
Das Bild wirkt auf den ersten Moment mit vielen Informationen gefüllt. Wir vereinfachen es etwas: Auf der rechten Seite ist eine Quelle, aus welcher Silberatome durch den Versuchsaufbau gesendet werden. In der Mitte befinden sich jeweils 2 Magnete, einmal (oben) mit einem Nordpol, einmal unten mit einem Südpol. Wichtig hierbei: Der Nordpol verläuft "V-Förmig" in Richtung des Silberatomstrahls, hat also eine etwas größere Auswirkung auf die Silberatome als das untere Süd-Magnetfeld. Nachdem die Atome durch den Apparat gesendet wurden, werden diese links detektiert. Auf dem Detektor wird festgestellt, wo die Silberatome auf dem Detektor auftreffen.
Hinweis aus der Schulzeit: Gleiches stößt sich ab. Wird der Nordpol eines Magneten gegen den Nordpol eines anderen Magneten gehalten, so stoßen sich die Magneten voneinander ab.
Wenn wir das Experiment nun mit dem Wissen, welches wir bisher gesammelt haben, einmal im Kopf durchgehen, so ergibt sich folgendes Bild: Je nachdem, wie das Magnetfeld des Silberatoms bei Eintritt in den Apparat ausgerichtet ist, so wird das Atom eher Richtung des oberen, oder eher Richtung des unteren Magneten abgelenkt. Die Silberatomquelle selbst nimmt keinerlei Ausrichtung vor - die Silberatome, welche den Versuchsaufbau durchlaufen, sind absolut zufällig ausgerichtet.
Das Video (Quelle: Jubobroff/ www.toutestquantique.fr/ veröffentlicht unter CC BY-SA Lizenz) zeigt bis zur 40. Sekunde sehr gut das Ergebnis, welches wir erwarten würden: Je nach Ausrichtung der Silberatome sollten diese eine gleichmäßige Linie auf dem Detektor ergeben. Was das Experiment jedoch ergeben hat, war ein anderes Bild. Das Video hat es bereits verraten: Die Silberatome haben sich in 2 Gruppen, entweder "oben" oder "unten", gruppiert. Hierfür ausschlaggebend ist das äußerste Elektron. Sobald wir die Achsen bzw. die Pole des Magnetfeldes des Atoms bestimmen ("messen"), so scheint sich das Elektron spontan dazu zu entscheiden, ob es jetzt "oben" oder "unten" auf den Detektor aufschlägt.
Anders formuliert: Messen wir das Elektron bzw. seinen Spin vertikal, wie im Video, so entscheidet es sich entweder dazu, den Nordpol (was ich zukünftig "Spin N in vertikaler Richtung" nenne werde), oder den Südpol "oben zu haben" ("Spin S in vertikaler Messrichtung").
Das Experiment ist nicht an eine vertikale Ausrichtung gebunden, wir können den Aufbau auch in jedem belieben Winkel drehen. Auch in einer horizontalen Messrichtung würden wir ein ähnliches Ergebnis vorfinden: Es würde zwei Gruppen geben. Eine Gruppe mit "Spin N in horizontaler Messrichtung", eine zweite Gruppe mit "Spin S in horizontaler Messrichtung".
Kapitel 3: Wiederholte Messungen
Richtig spannend wird es jedoch erst dann, wenn wir die Messungen wiederholen. Überlegen wir uns nachfolgend den folgenden Aufbau:
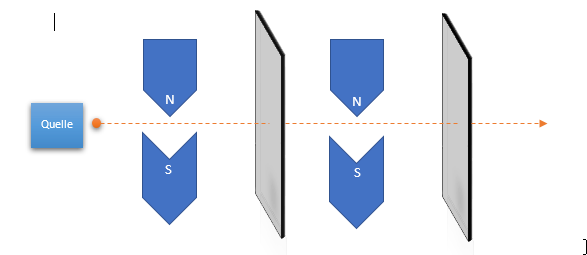
Die schematische Darstellung sollte zum Verständnis genügen, auch wenn sie eigentlich nicht ganz korrekt ist. Das Ergebnis hier ist vorhersehbar: Messe ich die gleiche Eigenschaft erneut, sollte das Ergebnis, wie in der klassischen Physik, wiederholbar sein. In dieser Aufstellung ist es dies auch. Wird beim ersten Detektor Spin N in vertikaler Richtung gemessen, so wird dieses Ergebnis auch beim zweiten Detektor gemessen.
Spannend wird das Experiment dann, wenn wir bei der zweiten Messung den Apparat um 90 Grad drehen:
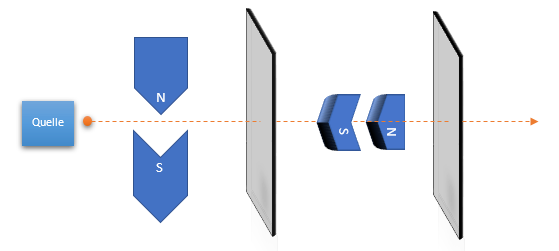
Wenn wir mehrere Silberatome mit einem Spin "N" durch beide Detektoren senden, so würden die Silberatome im ersten Detektor "unten" detektiert werden. Im zweiten Detektor jedoch, würden die Atome mit einer Wahrscheinlichkeit von 50% "rechts" oder mit einer Wahrscheinlichkeit von 50% "links" detektiert werden. Entgegen der klassischen Physik würde das Experiment auch bei exakt gleichen Voraussetzungen stets eine 50/50 Aufteilung im zweiten Detektor vorfinden lassen - das Experiment wäre somit nicht reproduzierbar. Das Ergebnis im zweiten Detektor ist auf den ersten Blick zufällig. Es gibt keine Möglichkeit, ein Silberatom bereits an der Quelle so zu präparieren, dass dieses im zweiten Detektor mit Sicherheit "rechts" oder "links" landen würde.
Wir halten fest: Messungen in gleicher Richtung führen stets zu gleichen Ergebnissen. Messungen, die nacheinander um 90° gedreht stattfinden, führen zu einem 50/50 Ergebnis im Rahmen der zweiten Messung. Doch was passiert, wenn wir den zweiten Apparat beispielsweise nur um 60° drehen würden?
Kapitel 4: Spin-Messungen in der Welt der Quantenphysik
Bevor wir uns dieser Frage widmen, müssen wir vorab kurz auf die Messungen eingehen. Anders als in der klassischen Physik haben Messungen an so kleinen Elementen, wie Atomen, eine Auswirkung auf das gemessene Objekt selbst. Würde unser Auto bei einer Geschwindigkeitskontrolle mit einer Lasermessung der Polizei mit einem Laserimpuls gemessen werden, so würde niemand auf die Idee kommen, dass der Laserimpuls die Geschwindigkeit unseres Autos spürbar verändert hat. In der Welt der aller kleinsten Teilchen gestaltet sich dies jedoch anders - eine Messung durchzuführen ohne das gemessene Objekt zu beeinflussen ist nicht möglich. Jede Messung führt stets zu einer Interaktion mit dem gemessenen Objekt.
Kommen wir zurück zur oberen Frage: Was passiert, wenn wir den zweiten Apparat im Winkel von 60° drehen? Hierbei ist es wichtig zu verstehen, dass wir in der Welt der Quantenphysik stets mit Wahrscheinlichkeiten arbeiten müssen.
Wir vereinfachen unseren Versuchsaufbau etwas:

Im Prinzip haben wir hier eine Blackbox, die mit "hier ist oben" beschriftet ist. Wir nehmen an, dass die Komponenten in der Box fest verbaut sind und die Box selbst, aus ihrer Perspektive, in dieselbe Richtung misst. Die Box gibt ein Messergebnis im grünen Kasten aus. Im Beispiel wäre der gemessene Spin "N".
Ein Beispiel:
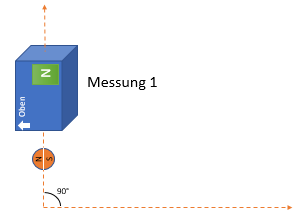
Die erste Messung ergibt "N".
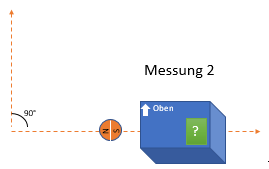
Die zweite Messung ergibt bei 90°, wie bereits erklärt, zu 50% ein "N" und zu 50% ein "S" aus.
Ein bisschen Mathematik: Die Wahrscheinlichkeit, in der zweiten Messung bei 90° erneut ein "N" zu erhalten, ist:
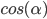 ,
,
im Falle der zweiten Messung somit:
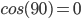
Das Ergebnis lässt sich wie folgt interpretieren:
- 1 = die Messung ergibt zu 100% ein N
- 0 = die Messung ergibt zu 50% ein N
- -1 = die Messung ergibt zu 0% ein N
Bei unserem oberen Beispiel: Drehen wir in der zweiten Messung die Blackbox um 60°, anstelle von 90°, so wäre das Ergebnis:
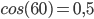
Auf einer Skala von -1 bis 1 bedeutet dies: Die Wahrscheinlichkeit, in der zweiten Messung erneut ein N als Ergebnis zu erhalten, liegt bei 3/4 oder 75%.
Kapitel 5: Das Wichtigste des ersten Beitrags
Abschließend möchte ich noch einmal die wichtigsten Elemente dieses Beitrags zusammenfassen:
Die Messungen in der Welt der Quantenphysik sind diskret
Entweder wir erhalten ein "dort ist Norden" oder ein "in exakt der anderen Richtung ist Norden". Andere Messergebnisse sind nicht möglich.
Messungen beeinflussen das Messobjekt
Durch eine Messung interagieren wir mit dem Messobjekt. Ein Beispiel: Um die Sache zu vereinfachen, nehmen wir an, ein Atom wäre zweidimensional und hätte, wie auf einer Uhr, seinen magnetischen Nordpol auf 2 Uhr. Würden wir nun eine Messung vornehmen, so müssten wir uns entscheiden. Wir könnten nun beispielsweise messen: Liegt der Nordpol auf 0 Uhr? Die Antwort wäre zu 75% ja (2 Uhr = 60° von 0 Uhr entfernt). Das Ergebnis der Messung programmiert das Atom jedoch auch auf exakt dieses Ergebnis: Der magnetische Nordpol wäre nun exakt bei 0 oder bei 6 Uhr, je nach Ergebnis. Eine zweite Messung hat das Ergebnis der ersten stets als Grundlage. Wir werden nach einer Messung nie mehr erfahren können, wo genau der magnetische Nordpol vor der Messung lag. In der klassischen Physik ist dies anders - eine Geschwindigkeitsmessung kann beliebig oft wiederholt werden, ohne dass dies das Ergebnis merklich beeinflusst.
Ergebnisse sind anhand von Wahrscheinlichkeiten vorhersagbar
Führe ich 10x exakt die gleiche Messung durch, so wird im Ergebnis der Spin 10x exakt gleich sein. Verändern wir jedoch den Versuchsaufbau, so kommen Wahrscheinlichkeiten zum Tragen. Bei einer Rotation um 90° könnten wir alle in der modernen Physik bestimmbaren Parameter ermitteln - wir wüssten dennoch nicht vorab, was in der zweiten Messung herauskommen wird. Dies ist eine fundamentaler Unterschied zur klassischen Physik - werfe ich dort beispielsweise eine Münze, so ist das Ergebnis nicht zufällig. Sobald ich in der Lage bin, alle relevanten Parameter ("Geschwindigkeit des Wegwerfens", Richtung der Vektoren, ...) mit einer ausreichenden Genauigkeit zu messen, so kann ich das Ergebnis vorhersehen.
Im nächsten Beitrag werden wir uns dem ersten kryptographischen Einsatzzweck aus dem Themengebiet des Quantencomputings bzw. der Quantenkryptographie annähern.
Quellen / Bildnachweis:
- Beitragsbild: © Peter Jurik/stock.adobe.com
- Video: Jubobroff/ www.toutestquantique.fr / CC BY-SA
- [1] Frank Behnsen at German Wikipedia / CC BY-SA
- [2] The American Institute of Physics credits the photo to AB Lagrelius & Westphal, which is the Swedish company used by the Nobel Foundation for most photos of its book series Les Prix Nobel.
- [3] Theresa Knott / CC BY-SA
