Nachdem mir die Frage gestellt wurde, warum ich im BLOG in einigen Beiträgen bestimmte Cipher empfohlen habe, möchte ich in diesem Beitrag auf die Bedeutung
- der Blockgröße und
- der Schlüssellänge
unter Berücksichtigung der bisher bekannt gewordenen Angriffsmöglichkeiten am Beispiel von Rijndael näher eingehen.
1 - Was ist die Blockgröße?
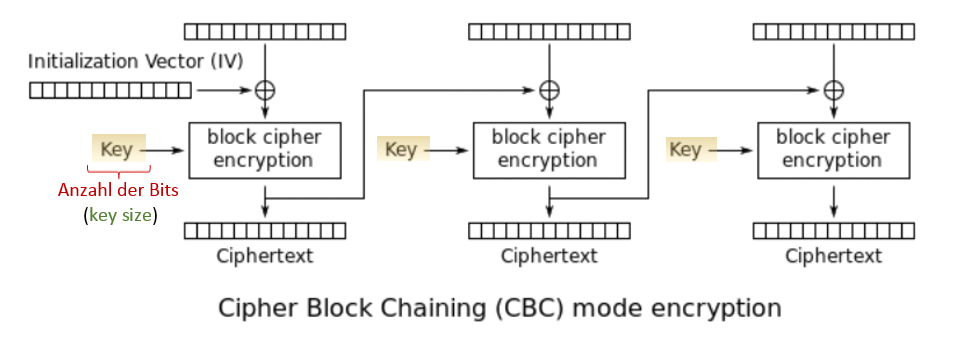
Die Blockgröße ist die Anzahl der Bytes, die, durch den Rijndael- Algorithmus, während eines Durchgangs verarbeitet werden können. Der Klartext wird hierbei durch einen Betriebsmodus wie CBC oder GCM in n Bit große Blöcke aufgeteilt und ggf. mit Hilfe von Padding- Verfahren aufgefüllt.
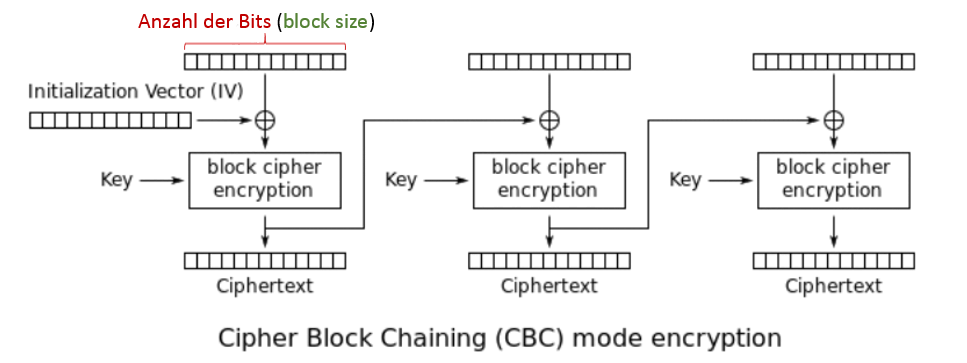
Der Rijndael- Algorithmus unterstützt verschiedene Blockgrößen (128, 160, 192, 224, und 256 Bits), im AES- Standard wird jedoch nur die 128-bit Blockgröße spezifiziert.
1.1 - Je größer die Blockgröße, desto besser?
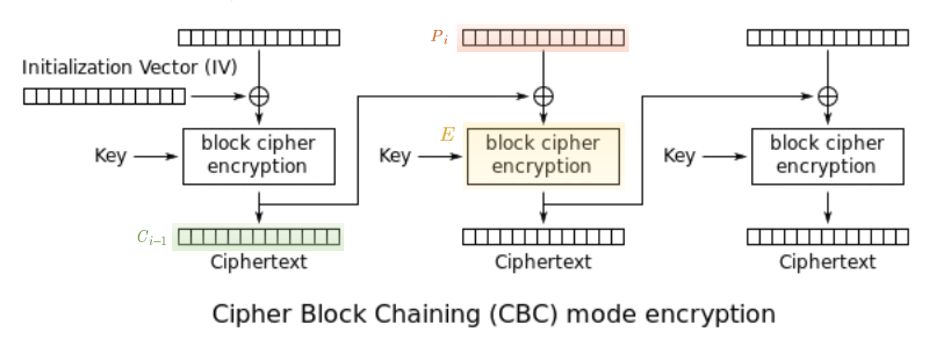
Kommt drauf an. Für die Sicherheit einiger Betriebsmodi ist es erforderlich, dass keine zwei Cipher-Text Blöcke mit demselben Inhalt generiert werden.
Leicht verdeutlicht werden kann dies mit Hilfe des Code-Book Angriffs:
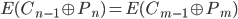
 sei hierbei ein Klartextblock,
sei hierbei ein Klartextblock,  der vorherige Cipher-Text Block und
der vorherige Cipher-Text Block und 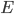 der Block Cipher.
der Block Cipher.
Da der Block-Cipher im CBC-Modus auf beiden Seiten mit demselben Schlüssel angewandt wird, kann dieser aus der Gleichung genommen werden,
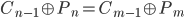
dies entspricht:
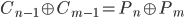 .
.
Naturgemäß liegt dem Angreifer der Cipher-Text vor, daher sind 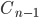 und
und 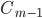 bekannt. Der Angreifer kennt somit die linke Seite der Gleichung, welche eine Konstante
bekannt. Der Angreifer kennt somit die linke Seite der Gleichung, welche eine Konstante 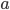 darstellt:
darstellt:
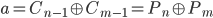 .
.
Wenn der Angreifer einen Teil des Klartextes kennt oder erraten kann, kann er sofort den korrespondierenden Teil des anderen Klartext-Blocks ableiten.
Hätte ein Algorithmus beispielsweise eine sehr kleine Blockgröße 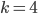 , bräuchte der Angreifer
, bräuchte der Angreifer 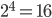 Einträge in seinem "code book" um das Chiffrat vollständig entschlüsseln zu können.
Einträge in seinem "code book" um das Chiffrat vollständig entschlüsseln zu können.
In der Praxis reichen jedoch, aufgrund des Geburtstagsparadoxons, meist 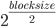 Blöcke um Kollisionen zu finden.
Blöcke um Kollisionen zu finden.
Die Verwendung einer kleineren Blocksize ist somit anfälliger für Attacken dieser Art. Der Data Encryption Standard hat beispielsweise eine Blocksize von 64 bit, was
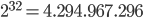
Blöcke ergibt, die benötigt werden, um wahrscheinlich eine Kollision zu produzieren, multipliziert mit der Blocksize von 64 bit,
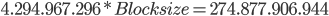
Bit an Daten, was etwa
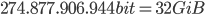
Klartext entspricht, was in der heutigen Zeit nicht viel ist.
Zum Vergleich: AES hat eine Blocksize von 128 bit, was
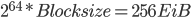
an Klartext entsprechen würde. Eine Blocksize von 256 bit würde bereits 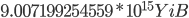 entsprechen.
entsprechen.
Die Rechenbeispiele verdeutlichen folgendes Zwischenfazit:
- Blöcke sollten, aus Sicht der Code-Book Attacken, gewissen Mindestlängen haben und
- Blockgrößen von 128bit oder gar mehr liegen statistisch weit außerhalb von dem, was anfällig für Attacken dieser Art wäre.
Auf Basis der bisherigen Erkenntnisse ist eine Blockgröße von 128 bit mehr als ausreichend! Zusammenfassend sollte beachtet werden, dass der AES Standard ausschließlich 128 bit Blöcke standardisiert hat, es ist somit davon auszugehen, dass diese Variante kryptoanalytisch deutlich besser analysiert wurde als die 256 bit Variante. Das offizielle AES Proposal stellt ebenfalls heraus, das Blockgrößen größer als 128 bit theoretisch mehr Angriffsfläche bieten könnten, als eine Blockgröße von 128 bit.
2 - Was ist die Schlüsselgröße?
Die Schlüsselgröße bezeichnet die Länge des verwendeten Schlüssels. Die Keysize findet sich im Namen von AES wieder:
- AES-128 beinhaltet einen Schlüssel mit einer Länge von 128 bit,
- AES-192 ... mit einer Länge von 192 bit und
- AES-256 ... mit einer Länge von 256 bit.
2.1 - Vom Nutzerpasswort zum AES-Key
Um den AES Key aus den Benutzerdaten (Passphrase, Keyfiles, ...) abzuleiten, wird meisten PBKDF2 (Password-Based Key Derivation Function 2) eingesetzt. PBKDF2 wendet auf die Benutzereingaben zusammen mit einem Saltwert eine pseudozufällige Funktion in mehreren Iterationen an.
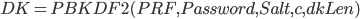
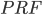 sei die pseudozufällige Funktion, das
sei die pseudozufällige Funktion, das  die Benutzereingabe, der
die Benutzereingabe, der 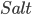 der kryptographische Salt,
der kryptographische Salt,  die Anzahl der Iterationen,
die Anzahl der Iterationen, 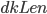 die Zielgröße des abgeleiteten Schlüssels.
die Zielgröße des abgeleiteten Schlüssels.
Die Anzahl der angewendeten Iterationen verringert die Gefahr von Brute-Force-Angriffen, der Salt senkt das Risiko von Rainbow-Tables. Das Verschlüsselungstool Truecrypt verwendet beispielsweise 512-bit Salts (=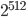 Möglichkeiten je Benutzerpasswort), HMAC-SHA-512, HMAC-RIPEMD-160 oder HMAC-Whirlpool als
Möglichkeiten je Benutzerpasswort), HMAC-SHA-512, HMAC-RIPEMD-160 oder HMAC-Whirlpool als 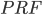 und
und 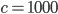 bzw.
bzw. 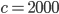 , je nach Hashfunktion.
, je nach Hashfunktion.
Anbei: Unter Linux wird die Anzahl der Iteration  von LUKS so gewählt, dass die Schlüsselableitung auf dem Rechner, auf dem die Passphrase gesetzt wird, etwa eine Sekunde dauert.
von LUKS so gewählt, dass die Schlüsselableitung auf dem Rechner, auf dem die Passphrase gesetzt wird, etwa eine Sekunde dauert.
Das Resultat der PBKDF2 Funktion ist ein AES Key mit zuvor definierter Keysize. Wird eine Cipher-Cascade eingesetzt (z.B. AES-Twofish-Serpent) ist es essentiell wichtig, dass die jeweils verwendeten Schlüssel voneinander unabhängig sind! Truecrypt realisiert dies für den genannten Beispiel-Cipher direkt über die initiale Schlüsselableitung mit 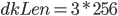 .
.
2.2 - Wie wird der AES-Key von AES verwendet?
Ohne zu tief in den AES- Algorithmus einzusteigen, ist es relevant zu wissen, das AES zu Beginn auf Basis des Keys eine so genannte Schlüsselexpansion durchführt, den Rijndael Key Schedule. Da dieser die Ausgangsbasis einiger bekannt gewordenen Attacken ist, werde ich diesen im Folgenden näher erläutern.
Beginnen möchte ich mit einigen einfachen, notwendigen Basis Operationen.
2.2.1 - Rcon
a) Die einfache Variante
Die AES-Rcon-Tabelle ist statisch, für Rijndael mit 128bit Blockgröße werden höchstens 11 Rundenschlüssel benötigt. Für die AES Varianten werden somit 10 weitere Rundenschlüssel benötigt, den ersten geben wir durch den Key selbst mit.
Aus diesem Grunde brauchen wir für die nächsten Operationen folgende 10 konstante Werte:
static const uint8_t Rcon[] = {
0x01, 0x02, 0x04, 0x08, 0x10, 0x20,
0x40, 0x80, 0x1B, 0x36 };
Wem dieses Wissen genügt, der kann den nächsten Punkt (b) überspringen.
b) Die vollständige Variante
Rcon greift intern auf einen endlichen Körper, einen Galoiskörper zurück. Da der Rijndael Algorithmus nur 8-bit große Zahlen erlaubt, hat der Galoiskörper die Größe von 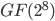 .
.
In AES-Implementierungen werden zur Berechnung gerne folgende Methoden verwendet:
uint8_t xtime(x)
{
return ((x << 1) ^ ((x & 0x80) ? 0x1B : 0x00));
}
for (i = 0, x = 1; i < 10; i++) {
Rcon[i] = x;
x = xtime(x);
}
Die Funktion xtime(x) funktioniert, in dem zuerst der übergebene Parameter x in eine 8-Bit große Nummer (Byte) konvertiert wird:
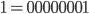
Die umgerechneten Bit Werte (0 oder 1) werden anschließend in der Reihenfolge 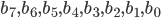 wie folgt dargestellt:
wie folgt dargestellt:
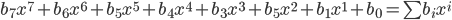 mit
mit 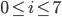
Einige Beispiele:
 identifiziert das spezifische endliche Feldelement
identifiziert das spezifische endliche Feldelement 
 identifiziert das spezifische endliche Feldelement
identifiziert das spezifische endliche Feldelement 
 identifiziert das spezifische endliche Feldelement
identifiziert das spezifische endliche Feldelement 
Anschließend erfolgt eine Multiplikation mit 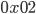 , was leicht durch einen Links-Shift auf Byteebene realisiert werden kann, im Beispiel (0x10 * 0x02),
, was leicht durch einen Links-Shift auf Byteebene realisiert werden kann, im Beispiel (0x10 * 0x02),
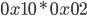
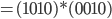
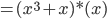
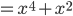
was gleichbedeutend wäre mit:
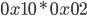
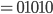
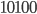
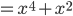
Da auf Basis endlicher Körper gerechnet wird, ist nach der Multiplikation zu prüfen, ob das 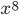 bit gesetzt ist, wenn ja, ist eine Reduktion mit dem unreduzierbaren Polynom des AES-Algorithmus notwendig:
bit gesetzt ist, wenn ja, ist eine Reduktion mit dem unreduzierbaren Polynom des AES-Algorithmus notwendig:
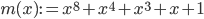
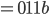 (Hexadezimal)
(Hexadezimal)
Im Beispiel:
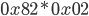
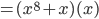
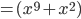
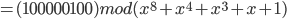
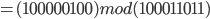

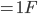
Somit ergibt
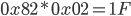
oder dezimal
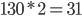
Der vollständige Körper würde wie folgt aussehen:
static const uint8_t Rcon[255] = {
0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8,
0xab, 0x4d, 0x9a, 0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3,
0x7d, 0xfa, 0xef, 0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f,
0x25, 0x4a, 0x94, 0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb, 0x8d,
0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab,
0x4d, 0x9a, 0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3, 0x7d,
0xfa, 0xef, 0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f, 0x25,
0x4a, 0x94, 0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb, 0x8d, 0x01,
0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d,
0x9a, 0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3, 0x7d, 0xfa,
0xef, 0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f, 0x25, 0x4a,
0x94, 0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb, 0x8d, 0x01, 0x02,
0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d, 0x9a,
0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3, 0x7d, 0xfa, 0xef,
0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f, 0x25, 0x4a, 0x94,
0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb, 0x8d, 0x01, 0x02, 0x04,
0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d, 0x9a, 0x2f,
0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3, 0x7d, 0xfa, 0xef, 0xc5,
0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f, 0x25, 0x4a, 0x94, 0x33,
0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb
};
2.2.2 - Rotate
Rotate ist deutlich einfacher: Hierbei wird jeweils ein 32-bit Wort um 8 Bit nach links rotiert, daher
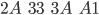
führt zu
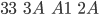
2.2.3 - S-Box
Eine Substitutionsbox kommt in vielen Algorithmen zum Einsatz, sie ist eine nichtlineare Substitutionsoperation, bei der eine m-stellige Binärzahl durch eine n-stellige Binärzahl ersetzt wird. Substitionsboxen können, je nachdem ob sie statisch (wie bei AES) oder dynamisch (z.B. Twofish) verwendet werden, die Kryptoanalyse deutlich erschweren.
a) Die einfache Variante
Wie bereits oben geschrieben, gibt es für die S-Box auch hier 2 konstante Tabellen. Wem dies reicht, der kann die Details im folgenden Punkt (b) überspringen.
/* Forward S-Box */
static const uint8_t SBox[256] = {
// 0 1 2 3 4 5 6 7 8 9 A B C D E F
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76, // 0
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, // 1
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15, // 2
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, // 3
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84, // 4
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, // 5
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8, // 6
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, // 7
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73, // 8
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, // 9
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79, // A
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08, // B
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, // C
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e, // D
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, // E
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 // F
};
/* Reverse S-Box */
static const uint8_t RSBox[256] = {
// 0 1 2 3 4 5 6 7 8 9 A B C D E F
0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb, // 0
0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb, // 1
0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e, // 2
0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25, // 3
0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92, // 4
0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84, // 5
0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06, // 6
0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b, // 7
0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73, // 8
0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e, // 9
0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b, // A
0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4, // B
0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f, // C
0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef, // D
0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61, // E
0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d // F
};
b) Die vollständige Variante
Die S-Box-Generierung habe ich für diesen Blog wie folgt in Delphi umgesetzt (angelehnt an eine C Implementierung):
procedure TForm1.DoCalc;
var
i: integer;
logtable: array [0..255] of byte; // Log table
exptable: array [0..255] of byte; // Log table
a, c, s, x: Byte;
begin
a := 1;
for i := 0 to 255 do
begin
// Exptable Value setzen
exptable[i] := a;
// Bitweise AND-Verknüpfung
c := a AND $80;
// Linksverschiebung
a := a SHL 1;
if (c = $80) then
begin
// Bitweises XOR
a := a xor $1b;
end;
// Bitweises XOR
a := a xor exptable[i];
// Logtable Value setzen
logtable[exptable[i]] := i;
end;
exptable[255] := exptable[0];
logtable[0] := 0;
// Alle 256 Werte generieren
for i := 0 to 255 do
begin
// 0 ist selbst invertierend
if i = 0 then
x := 0
else
x := exptable[(255 - logtable[i])];
s := x;
for c := 0 to 3 do
begin
// zirkulare Rotation nach Links
s := (s SHL 1) OR (s SHR 7);
// Bitweises XOR
x := x XOR s;
end;
// Bitweises XOR mit 0x63
x := x XOR 99;
// Ergebnis in ein Memo packen (siehe Screenshot)
Memo1.Text := Memo1.Text + '0x' + IntToHex(x, 2) + ', ';
end;
end;
Das Ergebnis sieht wie folgt aus:
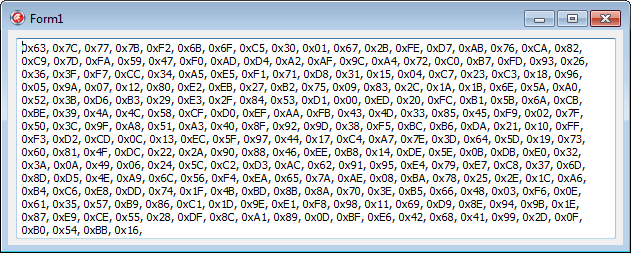
Der Code sollte selbsterklärend sein: Es wird zunächst jedes Byte, aufgefasst als Vertreter des endlichen Körpers 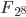 (= 8 Bit Größe eines Eintrags ->
(= 8 Bit Größe eines Eintrags -> 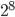 ), durch sein multiplikatives Inverses ersetzt, außer der 0, diese bleibt am Platz.
), durch sein multiplikatives Inverses ersetzt, außer der 0, diese bleibt am Platz.
Darauf folgend wird über 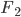 eine affine Abbildung als Matrixmultiplikation und Addition von
eine affine Abbildung als Matrixmultiplikation und Addition von 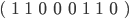 berechnet:
berechnet:

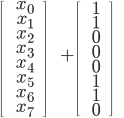
Das Ganze wirkt auf dem ersten Blick erst mal etwas unverständlich, wird aber relativ schnell klar, in dem man es einmal selbst durchrechnet. Ich selber (als Nicht-Mathematiker 🙂 ) hab mich anfangs daran gehalten, den oberen Code einmal von Hand auszurechnen - ziemlich schnell sollte dabei klar werden, wie die S-Box errechnet wird.
Ein guter Einstieg ist auch die Wikipedia zum Thema Rijndael's Finite Field.
2.2.4 - Die eigentliche Schlüsselexpansion (AES / Rijndael Key Schedule) am Beispiel von AES-128
Die folgende Graphik visualisiert den eigentlichen AES Key Schedule:
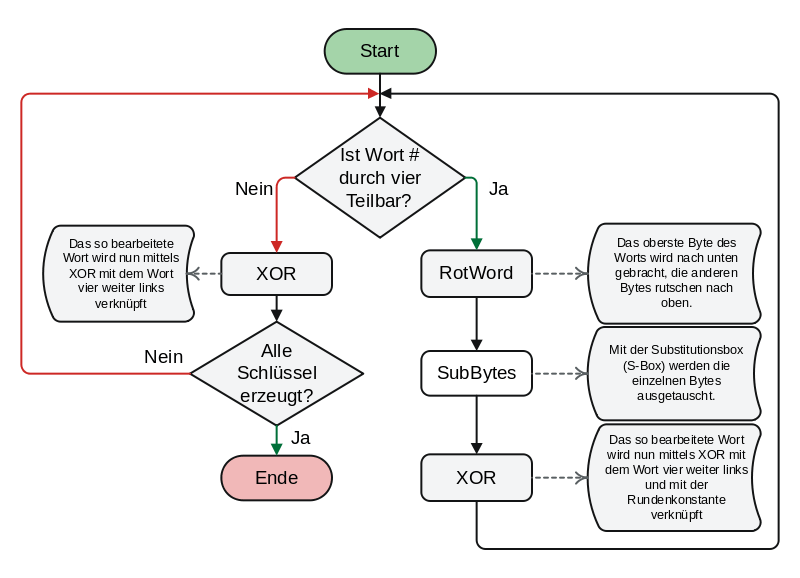
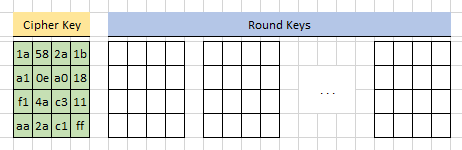
Im ersten Schritt wird der Key Schedule Algorithmus mit dem Cipher Key initialisiert:
Im nächsten Schritt wird geprüft, ob der Wort-Index durch 4 teilbar ist (in diesem Fall ja, da die Zählung bei 0 beginnt):
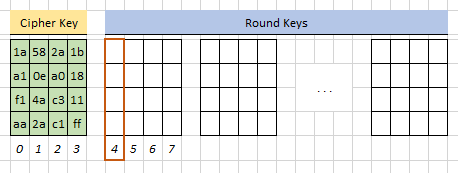
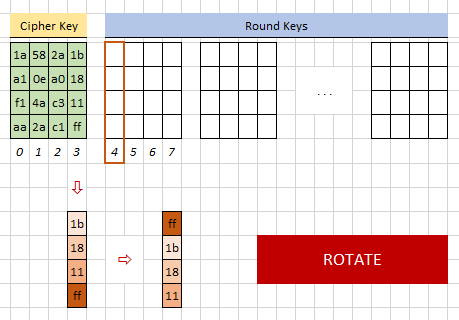
Das Wort 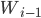 wird aus dem Cipher Key herausgenommen und rotiert:
wird aus dem Cipher Key herausgenommen und rotiert:
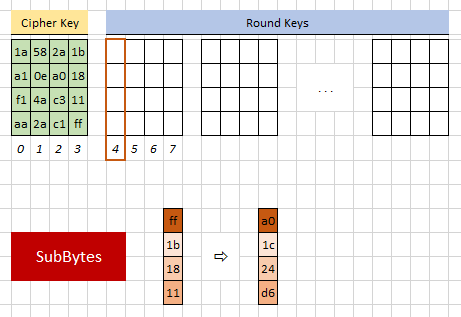
SubBytes, Anwendung der SBox:
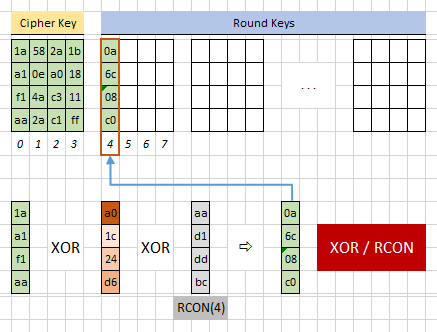
Anwendung XOR / RCON, Übernahme als Teil des Round Keys:
Die nächsten Wörter (5, 6 & 7) sind einfache XOR Operationen des vorherigen Worts mit dem Wort 4 vorher:
Alles in allem auch keine komplizierte Rechnung. Der Vorgang wird so lange wiederholt, bis alle notwendigen Rundenschlüssel generiert worden sind.
2.3 - Die Auswirkungen der AES Keysize auf den Key Schedule Algorithmus
Je nach verwendeter Keysize werden unterschiedliche Parameter auf den Key-Schedule Algorithmus angewandt:
- AES-128 verwendet die ersten 16 Byte des Cipher Keys direkt als Encryption Key. Der Schlüssel wird auf 176 Bytes expandiert.
- AES-192 verwendet die ersten 24 Byte des Cipher Keys direkt als Encryption Key. Der Schlüssel wird auf 208 Bytes expandiert.
- AES-256 verwendet die ersten 32 Byte des Cipher Keys direkt als Encryption Key. Der Schlüssel wird auf 240 Bytes expandiert.
Wird AES-256 angewendet, unterscheidet sich der Algorithmus leicht von der AES-128 und AES-192 Variante: Nach der erfolgreichen Generierung von 16 Byte, wird eine zusätzliche S-Box Substitution hinzugefügt.
Im Folgenden einige Beispiele, wie die Expansion eines Schlüssels, der nur aus 0-Zeichen besteht, aussieht:
AES-128
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 62 63 63 63 62 63 63 63 62 63 63 63 62 63 63 63 9b 98 98 c9 f9 fb fb aa 9b 98 98 c9 f9 fb fb aa 90 97 34 50 69 6c cf fa f2 f4 57 33 0b 0f ac 99 ee 06 da 7b 87 6a 15 81 75 9e 42 b2 7e 91 ee 2b 7f 2e 2b 88 f8 44 3e 09 8d da 7c bb f3 4b 92 90 ec 61 4b 85 14 25 75 8c 99 ff 09 37 6a b4 9b a7 21 75 17 87 35 50 62 0b ac af 6b 3c c6 1b f0 9b 0e f9 03 33 3b a9 61 38 97 06 0a 04 51 1d fa 9f b1 d4 d8 e2 8a 7d b9 da 1d 7b b3 de 4c 66 49 41 b4 ef 5b cb 3e 92 e2 11 23 e9 51 cf 6f 8f 18 8e
AES-192
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 62 63 63 63 62 63 63 63 62 63 63 63 62 63 63 63 62 63 63 63 62 63 63 63 9b 98 98 c9 f9 fb fb aa 9b 98 98 c9 f9 fb fb aa 9b 98 98 c9 f9 fb fb aa 90 97 34 50 69 6c cf fa f2 f4 57 33 0b 0f ac 99 90 97 34 50 69 6c cf fa c8 1d 19 a9 a1 71 d6 53 53 85 81 60 58 8a 2d f9 c8 1d 19 a9 a1 71 d6 53 7b eb f4 9b da 9a 22 c8 89 1f a3 a8 d1 95 8e 51 19 88 97 f8 b8 f9 41 ab c2 68 96 f7 18 f2 b4 3f 91 ed 17 97 40 78 99 c6 59 f0 0e 3e e1 09 4f 95 83 ec bc 0f 9b 1e 08 30 0a f3 1f a7 4a 8b 86 61 13 7b 88 5f f2 72 c7 ca 43 2a c8 86 d8 34 c0 b6 d2 c7 df 11 98 4c 59 70
AES-256
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 62 63 63 63 62 63 63 63 62 63 63 63 62 63 63 63 aa fb fb fb aa fb fb fb aa fb fb fb aa fb fb fb 6f 6c 6c cf 0d 0f 0f ac 6f 6c 6c cf 0d 0f 0f ac 7d 8d 8d 6a d7 76 76 91 7d 8d 8d 6a d7 76 76 91 53 54 ed c1 5e 5b e2 6d 31 37 8e a2 3c 38 81 0e 96 8a 81 c1 41 fc f7 50 3c 71 7a 3a eb 07 0c ab 9e aa 8f 28 c0 f1 6d 45 f1 c6 e3 e7 cd fe 62 e9 2b 31 2b df 6a cd dc 8f 56 bc a6 b5 bd bb aa 1e 64 06 fd 52 a4 f7 90 17 55 31 73 f0 98 cf 11 19 6d bb a9 0b 07 76 75 84 51 ca d3 31 ec 71 79 2f e7 b0 e8 9c 43 47 78 8b 16 76 0b 7b 8e b9 1a 62 74 ed 0b a1 73 9b 7e 25 22 51 ad 14 ce 20 d4 3b 10 f8 0a 17 53 bf 72 9c 45 c9 79 e7 cb 70 63 85
2.4 - Je größer die Keysize, desto besser?
Um diese Frage zu beantworten, müssen wir uns die wichtigsten beiden Kryptoanalysen näher anschauen.
2.4.1 - Biclique Attack
Quelle: Bogdanov, Khovratovich, Rechberger: Biclique Cryptanalysis of the Full AES
Bedingungen: Einige wenige Klartext-Geheimtext-Paare werden für den Angriff benötigt.
Auswirkungen: Der Angriff ist etwa um den Faktor 4 schneller als ein vollständiges Durchsuchen des Schlüsselraumes:
 in
in  Schritte,
Schritte, in
in  Schritte und
Schritte und in
in  Schritte.
Schritte.
Aufgrund der wenigen, notwendigen Bedingungen gilt der Biclique Angriff auf AES bis heute als Maßstab für die "praktische" Sicherheit der verschiedenen AES Varianten.
2.4.2 - Related-key-Attack (nur AES-192 und AES-256)
Quelle: Biryukov and Khovratovich: Related-key Cryptanalysis of the Full AES-192 and AES-256
Bedingungen: Der Angreifer benötigt den Klartext zu einer größeren Menge Chiffraten, deren Schlüssel auf bestimmte Weise in Verbindung stehen. Diese Bedingungen kommen in der Praxis meist nur bei Festplattenverschlüsselungen oder bei unsauberer Implementierung des gesamten Verschlüsselungs-Algorithmus vor.
Auswirkungen: Der Angriff reduziert die notwendigen Schritte zur Entschlüsselung wie folgt:
 in
in  Schritt und
Schritt und in
in  Schritte.
Schritte.
Dem Angriff liegt zu Grunde, dass die längeren Schlüssel dem Kryptologen mehr Möglichkeiten bieten, mathematischen Beziehungen konkretisieren zu können.
3 - Fazit
AES bleibt, unabhängig der Keysize - berechnungssicher. Die bisher erfolgten Angriffe kommen bei weitem nicht in eine Größenordnung, die praxisrelevant wären, zumal der letzte Angriff ein Angriff mit reduzierter Rundenzahl war. Welcher Algorithmus verwendet werden sollte, bleibt jedem selbst überlassen: Sicher sind alle 3 Varianten. Die bekanntesten Kryptographen haben zu dem Thema unterschiedliche Meinungen. Häufig kritisiert wird insbesondere das sehr einfache AES Key Schedule Verfahren.
Um die Sicherheit des AES Verfahrens zu erhöhen, wird über eine Erhöhung der Rundenzahl diskutiert, aktuell liegt die Sicherheitsmarge bei, je nach Keysize, gerade einmal drei Runden! In der Kryptographie geht es primär um Sicherheitsmargen: Wenn es möglich ist 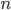 Runden eines Ciphers zu knacken, sollte der Cipher mindestens mit
Runden eines Ciphers zu knacken, sollte der Cipher mindestens mit 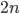 oder
oder 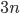 Runden versehen werden.
Runden versehen werden.
Wer ganz sicher gehen möchte, kann eine Verschlüsselungs-Cascade, z.B. aus Serpent und AES in Betracht ziehen. Essentiell wichtig ist hierbei jedoch, dass die jeweils verwendeten Schlüssel absolut unabhängig voneinander sind!
Bildnachweis:
- © alphaspirit - Fotolia.com
- [1] Das Bild ist Public Domain / Anlehnung an Quelle: https://en.wikipedia.org/wiki/File:CBC_encryption.svg
- [2] Das Bild steht unter der Creative Commons Attribution-Share Alike 3.0 Unported Lizenz / Autor: Stefan-Xp / https://commons.wikimedia.org/wiki/File:Schluesselexpansion-AES.svg


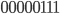
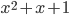
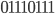
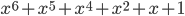
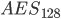
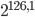
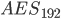
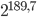
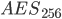
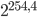
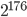
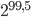
Sehr interessanter Artikel mal wieder, erklärt auch für Laien sehr gut!